Part 1 of Congruent Figures 4.1
Part 2 of Congruent Figures Proving Triangles Congruent
The third part of this series about congruent figures is proving triangles congruent. At this point, there is only one way to prove triangles congruent, with the definition of congruent triangles. Congruent triangles have 3 pairs of corresponding angles and 3 pairs of congruent angles. So, to prove two triangles congruent, we must establish that all 3 pairs of corresponding sides and angles are congruent.
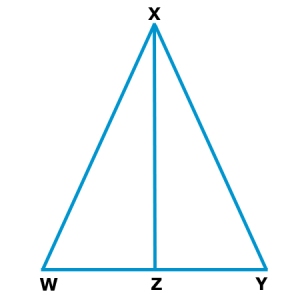
Given: segment WX is congruent to YX, segment WZ is congruent to segment YZ, angle W is congruent to angle Y and segment XZ is perpendicular to segment WY
Prove: triangle WXZ is congruent to triangle YXZ
With the given information: segment WX is congruent to YX, segment WZ is congruent to segment YZ, angle W is congruent to angle Y and segment XZ is perpendicular to segment WY, prove triangle WXZ is congruent to triangle YXZ. First, segment XZ is congruent to segment XZ by the reflexive property of congruence. Angles XZW and XZY are right angles by the definition of right angles. Angle XZW and angle XZY are congruent because all right angles are congruent. Angle WXZ is congruent to angle YXZ by the third angle theorem. It can be established that triangle WXZ is congruent to triangle YXZ by the definition of congruent triangles.
Filed under: Geometry, Proving Triangles Congruent | Tagged: Geometry, Proving Triangles Congruent, reflexive property of congruence, third angle theorem | Leave a comment »